General information

The main goal of the conference is to reflect recent significant events in the development of Algebraic Graph Theory (AGT) and related areas of mathematics. In particular it will commemorate the 50th anniversary of the discovery of a polynomial-time algorithm for the computation of the coherent closure of a given graph. Over the years, this algorithm has played a significant role in both AGT and computer science.

The programme of WL2018 will consist of

• a two-hour tutorial (Laci Babai)
• eight one-hour keynote lectures
• six 40-minutes invited session lectures, given by representatives of the younger generation of experts in AGT
• a limited number of 25-minutes contributed talks
• a limited number of short (5-10 minutes) presentations and
• a special session devoted to the history of the theory of coherent configurations.

The main preference in selection of contributed talks to be accepted will be given to talks in the area of AGT, those which reasonably correlate with the mainstream lines in AGT, reflected in the plenary lectures.

• László Babai: Coherent configurations and the graph isomorphism problem,
• Peter Cameron: Some old and new problems, related to primitive permutation groups,
• Edwin van Dam: Distance regular graphs in the framework of spectral graph theory,
• Tatsuro Ito: P and Q polynomial schemes and prospects in their classification,
• Mikhail Muzychuk: Isomorphism problem for Cayley objects,
• Dmitrii Pasechnik: Twisted Y-presentations in context of finite quotients of hyperbolic Coxeter groups,
• Ilia Ponomarenko: Schurian vs non-Schurian association schemes,
• Sergey Shpectorov: Current status of Majorana, Matsuo and Axial algebras.

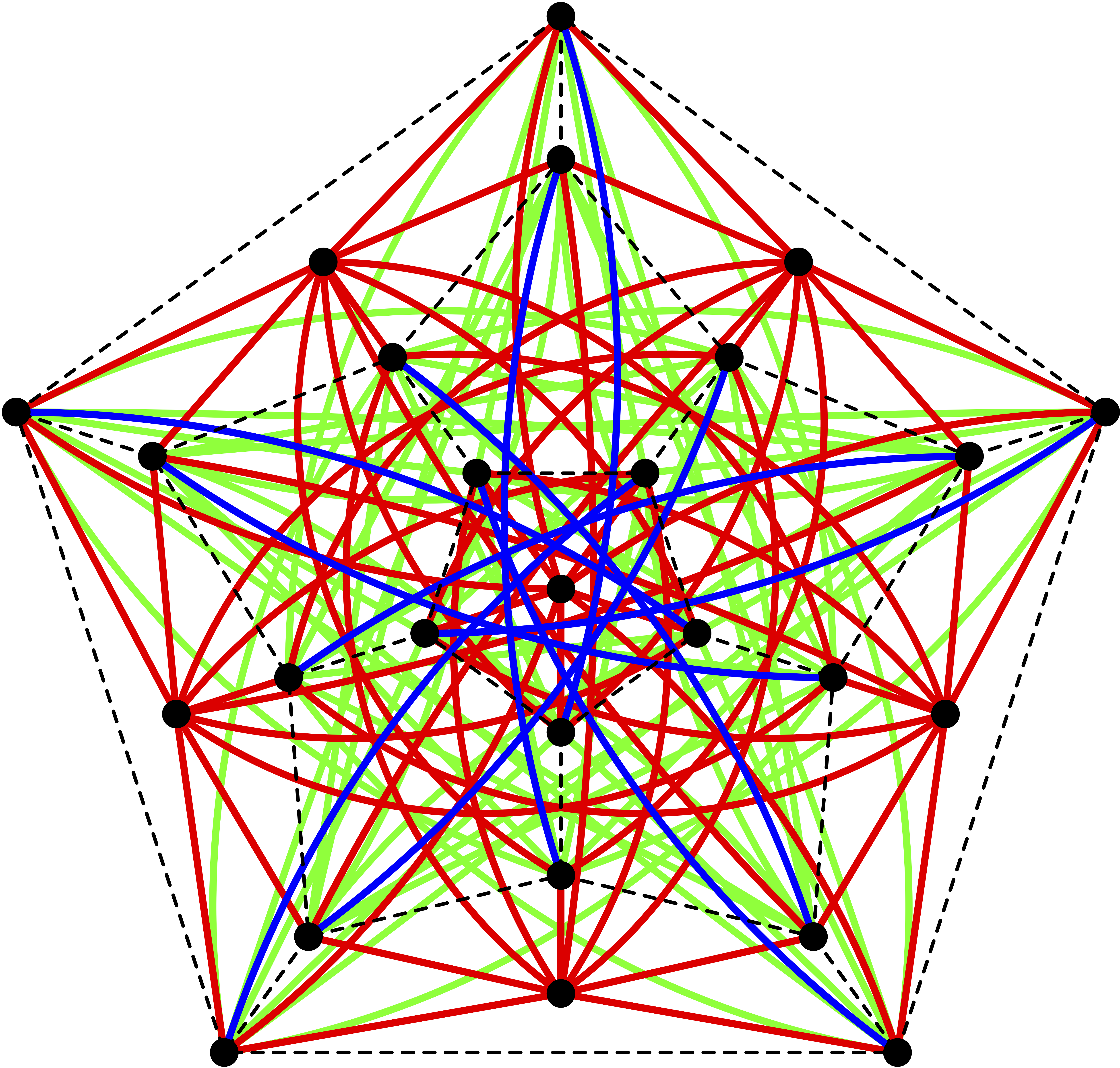
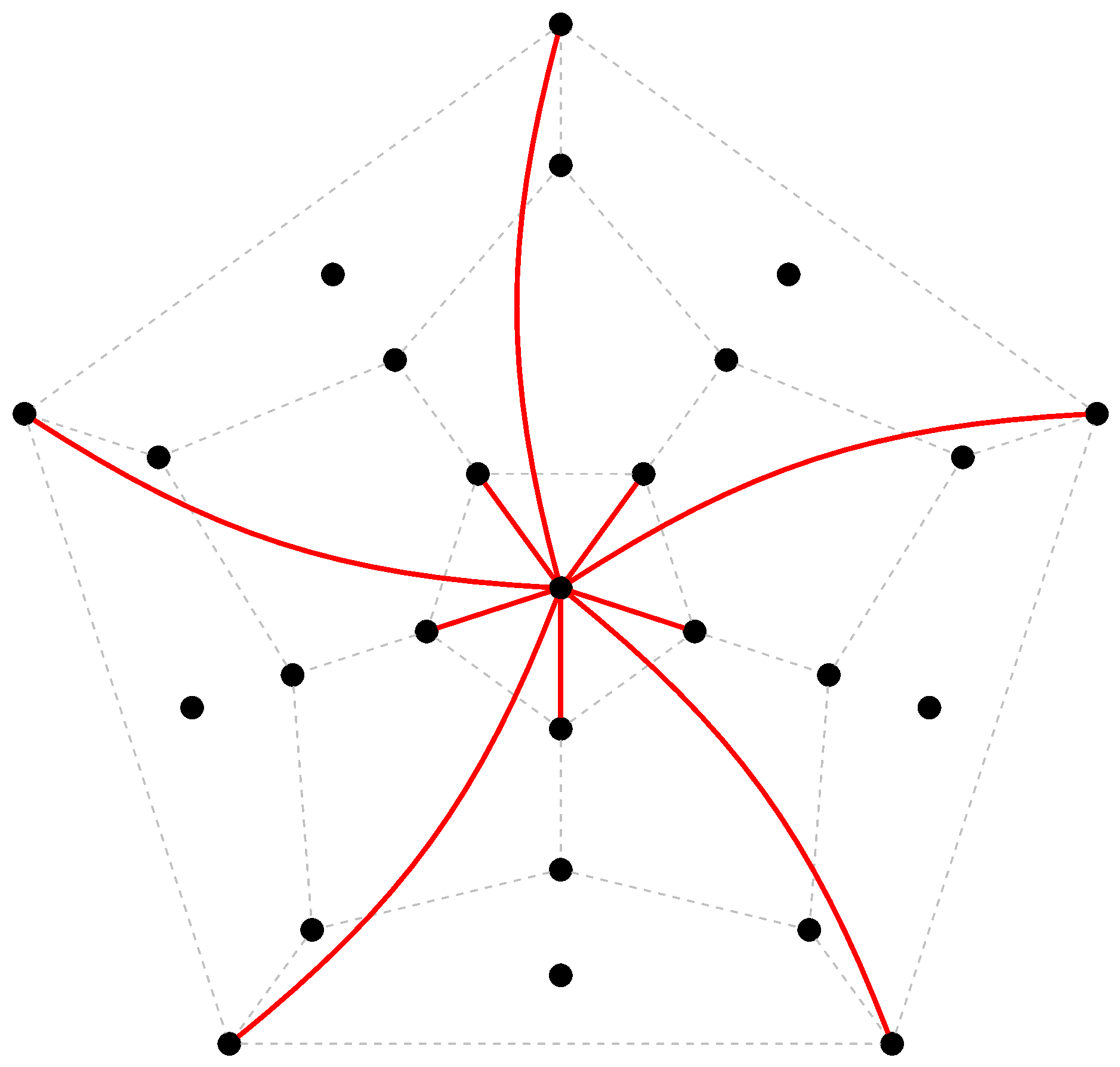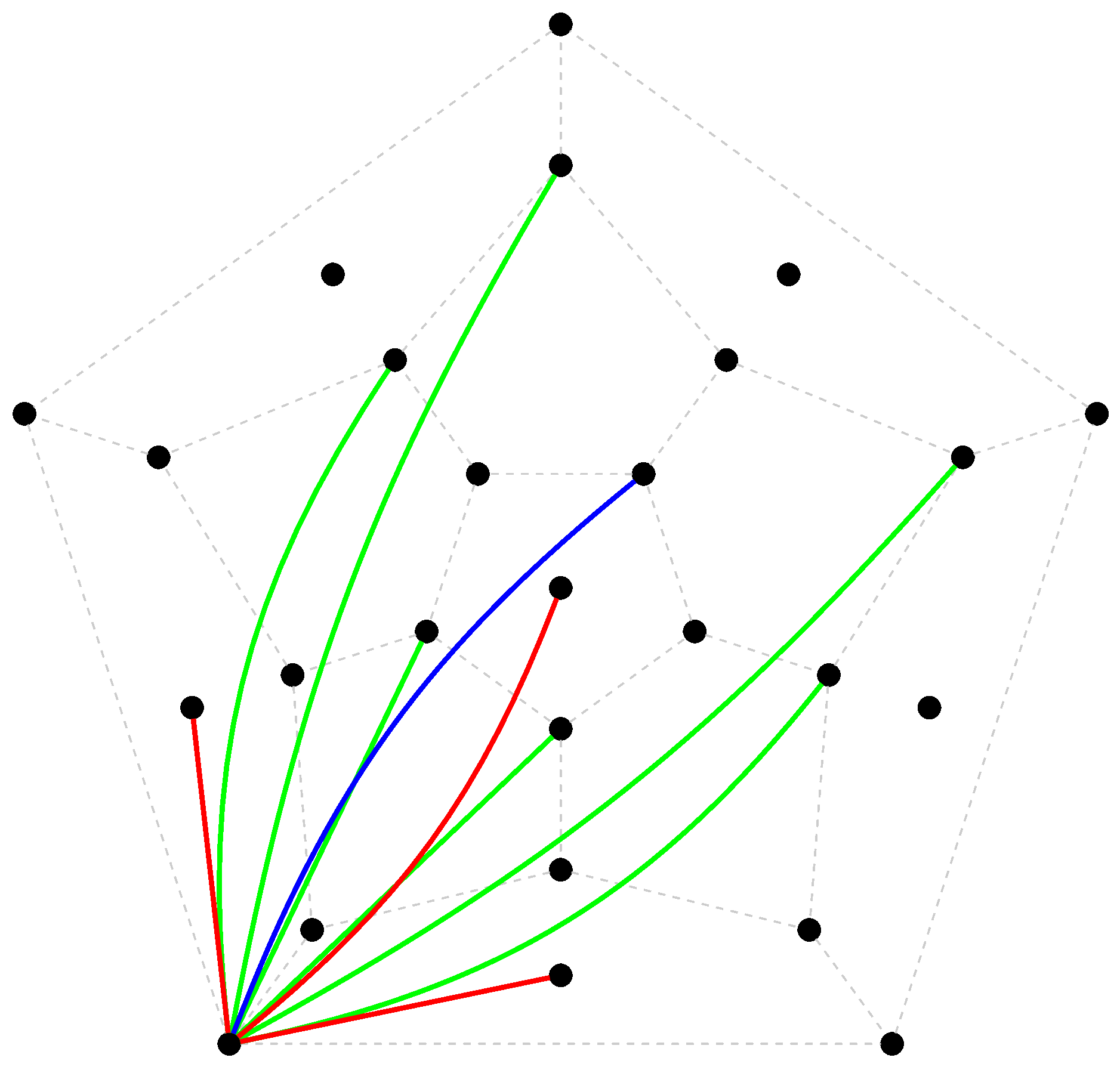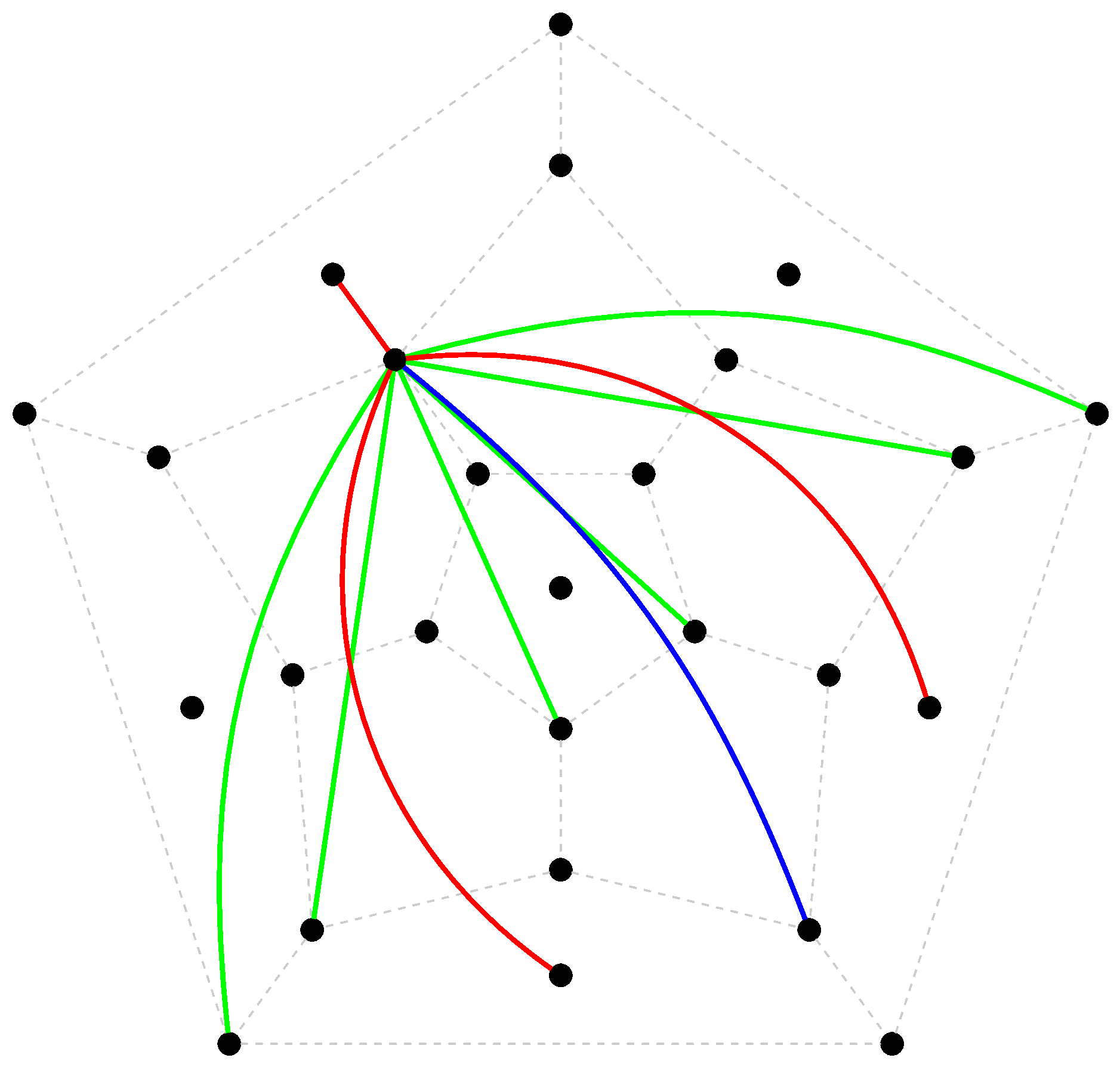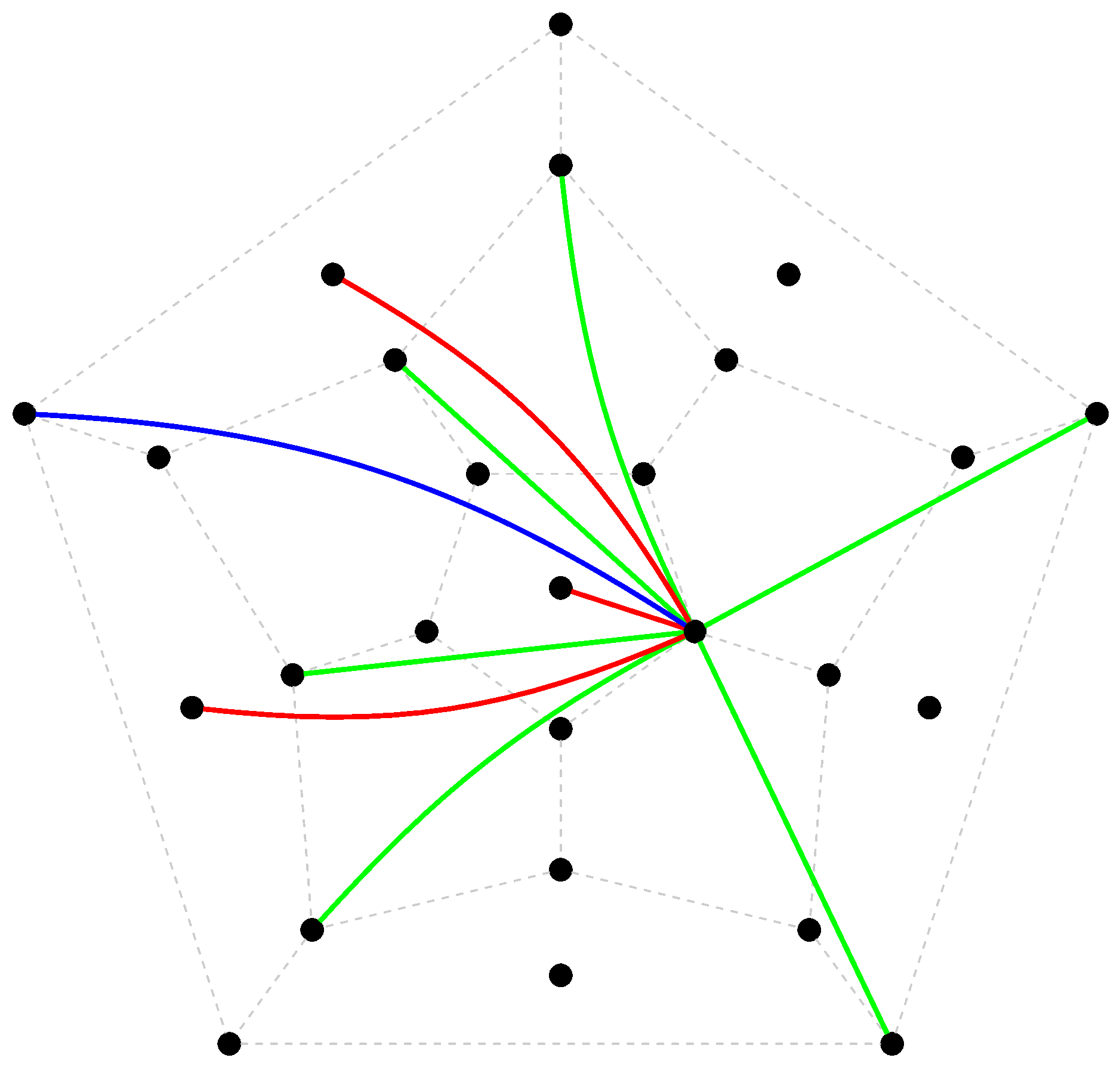
The Paulus-Rozenfeld-Thompson graph $T$ was independently discovered at least three times at Eindhoven (1973), Moscow (1973) and Tucson (1979). It is one of the ten strongly regular graphs (SRGs) with the parameters $(v, k, \lambda, \mu)=(26,10,3,4)$ . Among these $10$ graphs the SRG $T$ has the largest group $\mathrm{Aut}\,T$ of order $120$ , which is isomorphic to $A_5 \times Z_2$, the full symmetry group of the dodecahedron $\Delta$, regarded as a distance transitive graph.

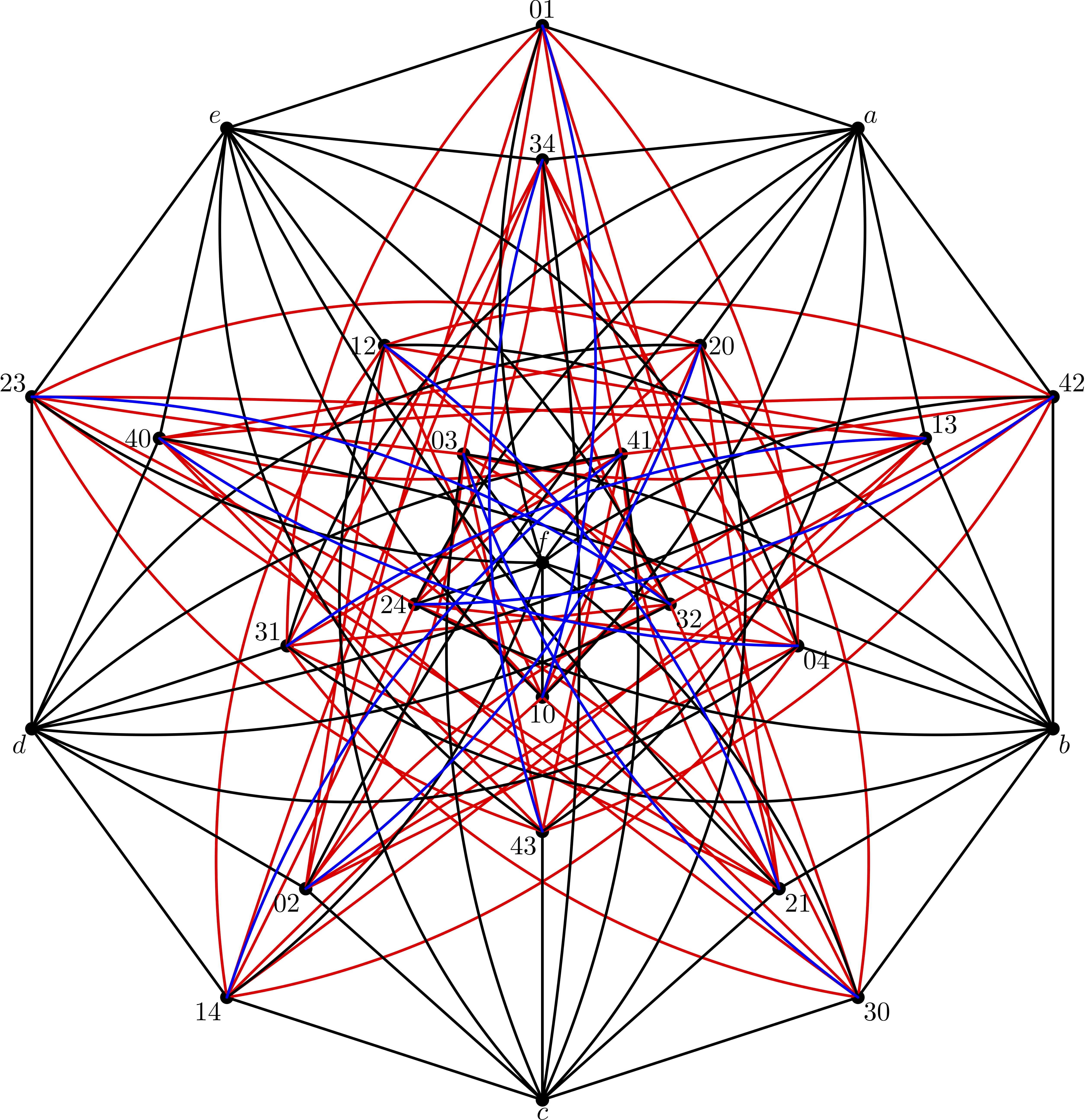
In modern terms, $T$ appears as merging of relations of rank $14$ coherent configuration $W$, namely $2$-orbits of the induced intransitive action $(A_5, C_1 \cup C_2)$ with two fibers of length $20$ and $6$. The fiber $C_1$ consists of all ordered pairs $(a,b)$ from the interval $[0,4]$. The fiber $C_2$ consists of the six images of the pentagon $([0,4],\{\{0,1\},\{1,2\},\{2,3\},\{3,4\},\{0,4\}\})$ under action of $(A_5, [0,4])$. There are three kinds of edges in the SRG $T$:

• edges in distance $3$, graph $\Delta_3$;
• edges in distance $5$, graph $\Delta_5$;
• edge between pair $(a,b)$ and pentagon $X$, provided $\{a,b\}$ is edge in $X$.

The diagram presents visual description of the SRG $T$, as merging of $W$, on the canvas of $\Delta$ with six extra vertices, corresponding to the pentagons with nodes from $[0,4]$. Different colors correspond to different orbits of $A_5$ on the edges of $T$.

A more detailed description of this Logo can be found in the article Animated logo of WL2018 (a shotcut to the animation). The logo is created by a team of organizers, consisting of Štefan Gyürki, Mikhail Klin and Matan Ziv-Av.

Conference photo